The BMI (body mass index) is a well known formula to put the weight of a person in relation to their size. It does only work well in a small range and fails on muscular people, but at least with one small trick we can remove the influence of muscle.

Historical reason for BMI

BMI is a very simple formula.

BMI = weight/height^2 where weight is measured in kg and height in m, as it should be.

But why the quadratic exponent you might ask? Doesn't allometry suggest a fractional exponent? True. But when BMI was invented in 1832, fractional exponents were mindblowingly hard.

On the other hand, you can just calculate the square of any decimal you encounter when measuring humans in your head pretty easily. Or on any non-scientific calculator.

FFMI and adjusted FFMI

FFMI is the abbreviation for Fat Free Mass Index. Trying to find a formula for FFMI is not that easy as one would expect. There are weird formulae all around, mostly because of freedom units and people not thinking about what they are doing. What the actual fuck, because the formula is not that hard:

FFMI = lean bodymass/height^2. It is just the same as BMI, you only replace total body mass by lean body mass.

In the infamous Kouri et al paper estimating FFMI of steroid users a linear normalization term is used for the FFMI to adjust for height, leading to the normalized FFMI (nFFMI) given by nFFMI = FFMI + 6.1*(1.8 - height) so that everything is normalized to the height of a 1.8m man.

There are two important notes about this formula.

The first is that this correction term has been created ad hoc for the study by calculating the slope of a regression line through the non-steroid users with an FFMI of 22 and above. Which is valid in the context of the study, but well, definitely not something that should be extended to the whole population unquestioned, like most people seem to do. The second is that the abstract reports a correction factor of 6.3, whereas the study uses 6.1 and I have seen both in use.

I don't think it's sensible to use a linear regression factor based upon a small, biased sample size and probably any correction is as valid or invalid as any other until we build a model that actually works on large datasets and ideally is not just a stupid curve fit (I am looking at you, DOTS and Wilks¹).

BMI decomposes into FFMI and FMI

By using FMI = fat mass/height^2 we can define the fat mass index and then indeed we get a linear decomposition of BMI:

BMI = FFMI + FMI

In particular we know that lifting people have FFMIs 3-8 points above genpop, ranging from about 20 - 25, with some individuals scoring even higher. If you lift you can gauge how advanced you are and adjust your BMI threshholds accordingly.

Note however that bodyweight alone is a risk factor just due to inconveniences like hydrostatic pressure, so if your BMI is beyond 30 or even 35, you have to closely monitor corresponding health markers, regardless of being fat or not. ²

I guess nobody really tries to adjust for gender or height using the BMI

The usual rules are 20-25 is ok, 25-30 is overweight but not critical, over 30 is fat and under 20 is underweight, with some more categorizations of the problematic cases as you move up or down towards death. However, they do not account for gender or height, despite the obvious implications of both, which becomes even more obvious with the decomposition of BMI into FFMI and FMI.

I have not come across a single attempt to adapt the guidelines, like using lower numbers for small females or bigger numbers for tall males. Maybe that is too easy. Maybe physical practitioners just do that in their offices and then have to do additional paperwork for the insurance side of things.

But more likely people which do not have the default body, which is "average sized sedentary adult human male" just get worse treatment. As always.

New BMI or BBMI for the rescue maybe

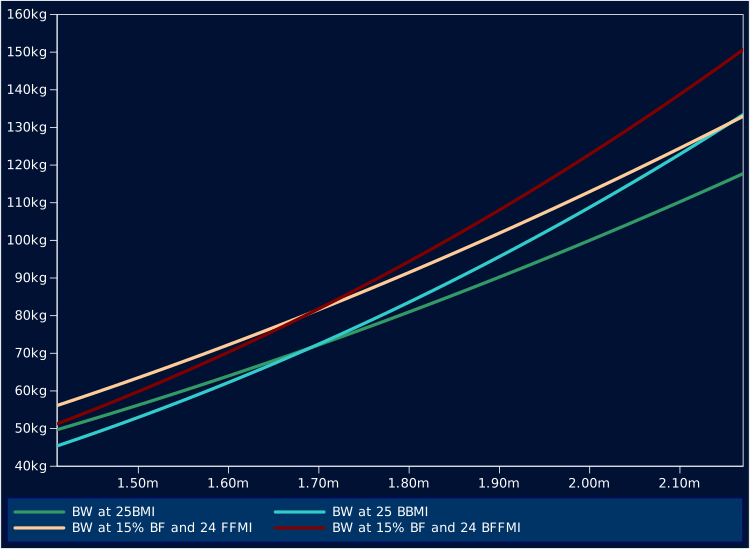
The obvious solution is just to scrap the BMI and use something with a fractional exponent, because we have computers. We will still not have perfect results with any simple formular, so we might as well take 2.5 as exponent midway between quadratic and cubic and it will be close enough anyway.

To keep the guidelines, one needs a normalizing factor to make "average sized adult human males" score the same number as before, i.e. something along the lines of 1.75^2.5/1.75^2 which is roughly equal to 1.3.

Tadaa, we have arrived at the "new BMI" or, even catchier, "Better BMI", which obviously is defined as BBMI = 1.3 * weight/height^2.5.

This is still linear in weight, so we could still use this to define a BFFMI and a BFMI and possibly this might just work well enough.

Or we can just use this to adjust our BMI tables.

Just looking at the following plot at least it seems to line up better with bodyweights observed in the wild and it is also roughly matching common optimal weight classes such as those suggested by Boris Sheiko, putting people in between 1.8m and 1.9m in the 110kg+ category.